More than spins: Exploring uncharted territory in quantum devices.
Many of today’s quantum devices rely on collections of qubits, also called spins. These quantum bits have only two energy levels, the ‘0’ and the ‘1’. However, spins in real devices also interact with light and vibrations known as bosons, greatly complicating calculations. In a new publication in Physical Review Letters, researchers in Amsterdam demonstrate a way to describe spin-boson systems and use this to efficiently configure quantum devices in a desired state.
Source: UvA/IoP news by Jans Henke.

Quantum devices use the quirky behaviour of quantum particles to perform tasks that go beyond what ‘classical’ machines can do, including quantum computing, simulation, sensing, communication and metrology. These devices can take many forms, such as a collection of superconducting circuits, or a lattice of atoms or ions held in place by lasers or electric fields.
Regardless of their physical realisation, quantum devices are typically described in simplified terms as a collection of interacting two-level quantum bits or spins. However, these spins also interact with other things in their surroundings, such as light in superconducting circuits or oscillations in the lattice of atoms or ions. Particles of light (photons) and vibrational modes of a lattice (phonons) are examples of bosons.
Unlike spins, which have only two possible energy levels (‘0’ or ‘1’), the number of levels for each boson is infinite. Consequently, there are very few computational tools for describing spins coupled to bosons. In their new work, physicists Liam Bond, Arghavan Safavi-Naini and Jiří Minář of the University of Amsterdam, QuSoft and Centrum Wiskunde & Informatica work around this limitation by describing systems composed of spins and bosons using so-called non-Gaussian states. Each non-Gaussian state is a combination (a superposition) of much simpler Gaussian states.
Each blue-red pattern in the image above represents a possible quantum state of the spin-boson system. “A Gaussian state would look like a plain red circle, without any interesting blue-red patterns,” explains PhD candidate Liam Bond. An example of a Gaussian state is laser light, in which all light-waves are perfectly in sync. “If we take many of these Gaussian states and start overlapping them (so that they’re in a superposition), these beautifully intricate patterns emerge. We were particularly excited because these non-Gaussian states allow us to retain a lot of the powerful mathematical machinery that exists for Gaussian states, whilst enabling us to describe a far more diverse set of quantum states.”
Bond continues: “There are so many possible patterns that classical computers often struggle to compute and process them. Instead, in this publication we use a method that identifies the most important of these patterns and ignores the others. This lets us study these quantum systems, and design new ways of preparing interesting quantum states.”
The new approach can be exploited to efficiently prepare quantum states in a way that outperforms other traditionally used protocols. “Fast quantum state preparation might be useful for a wide range of applications, such as quantum simulation or even quantum error correction,” notes Bond. The researchers also demonstrate that they can use non-Gaussian states to prepare ‘critical’ quantum states which correspond to a system undergoing a phase transition. In addition to fundamental interest, such states can greatly enhance the sensitivity of quantum sensors.
While these results are very encouraging, they are only a first step towards more ambitious goals. So far, the method has been demonstrated for a single spin. A natural, but challenging extension is to include many spins and many bosonic modes at the same time. A parallel direction is to account for the effects of the environment disturbing the spin-boson systems. Both of these approaches are under active development.
Publication
Liam J. Bond, Arghavan Safavi-Naini and Jiří Minář, Fast quantum state preparation and bath dynamics using non-Gaussian variational Ansatz and quantum optimal control. Physical Review Letters 132, 170401 (2024).
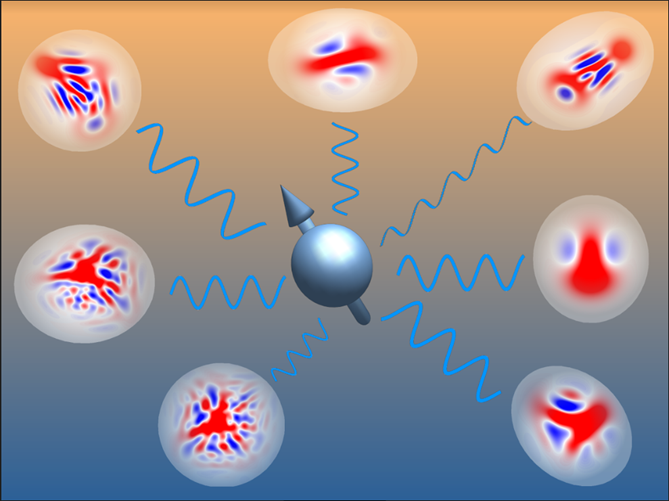
Caption: A spin (blue ball with arrow) interacts with the surrounding bosons described by non-Gaussian states – a new computational method to accurately describe what happens inside quantum devices. Credit: Jiří Minář
